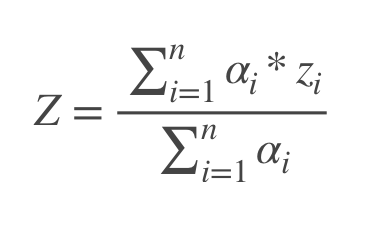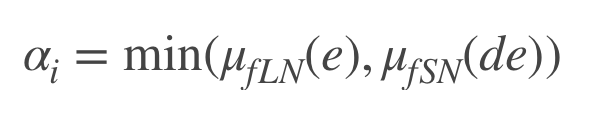Коллеги, продолжим реализацию регулятора, основанного на нечеткой логике.
В прошлой статье мы разобрали все нужные сущности и ввели операции над ними.
Теперь давайте уже разговаривать более предметно, в терминах нашей задачи и ее реализации. Как всегда имеется и видеоверсия выпуска https://youtu.be/TyYKEoPJieA, подписывайтесь, делитесь и ставьте лайки).
Итак, возьмем универсальное множество X, на котором мы будем строить все наши нечеткие подмножества, равным отрезку [-125,125]. Элементами этого универсума будут целые числа.
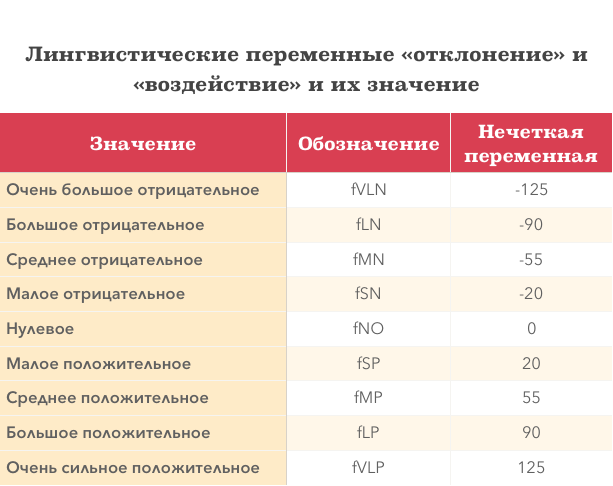
Введем следующие лингвистические переменные для выравнивания нашего БПЛА по крену:
Таким образом мы ввели 4 значения для отрицательного левого крена, 4 — для правого крена и одно значение, обозначающее отсутствие крена. Эти значения (нечеткие множества) относятся в равной степени к лингвистическим переменным «Отклонение» и «Воздействие». Вообще, можно для этих переменных задавать разные значения, но мы, чтоб упростить задачу, будем использовать один набор значений.
Ну вроде осталось самая малость, создать
Правила нечеткого регулирования
Итак, что из себя представляют нечеткие правила. Это конструкции вида
IF <условие> THEN <воздействие>
которые накладывают на процесс регулирования некую логику.
Иными словами, мы берем эксперта и уточняем у него, что делать в той или иной ситуации, и записываем это в виде правил.
Например:
Если у нас сильный крен влево, и предыдущий крен был тоже большим, то мы даем сильный крен вправо.
Как мы это запишем в наших лингвистических переменных:
IF e = fVLN AND de = fSN THEN z=fVLP
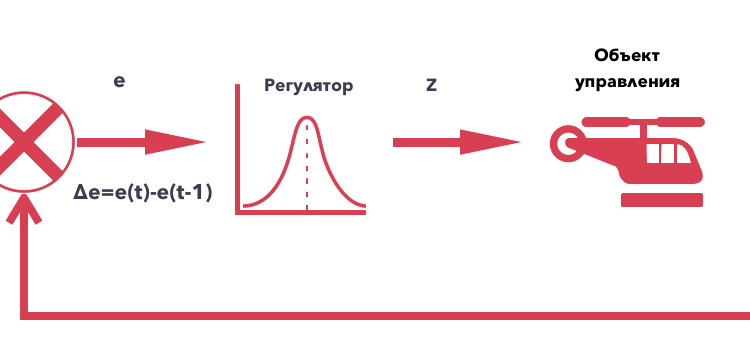
где e — это текущая ошибка регулирования, а de — это первая разность ошибки в текущий дискретный момент. Через z — мы обозначаем управляющее воздействие на объект управления. Смотрим схему в заголовке статьи.
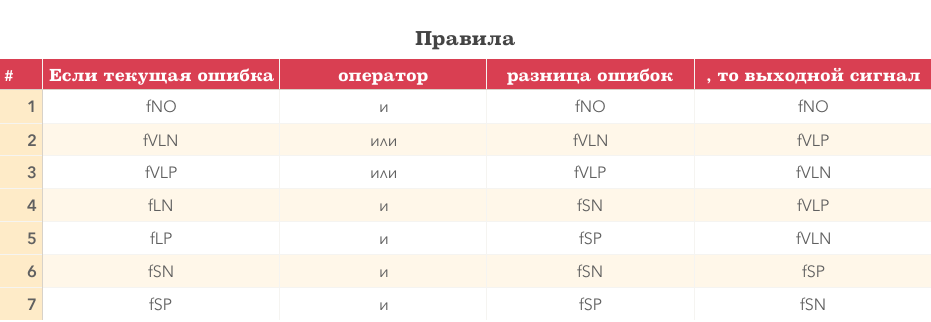
Итак, мы опросили специалиста и записали набор правил для управления дроном. Получился какой-то набор правил, ну скажем вот такой:
Ура, мы сделали практически всю основную работу, остался пустяк)
Нечеткий вывод
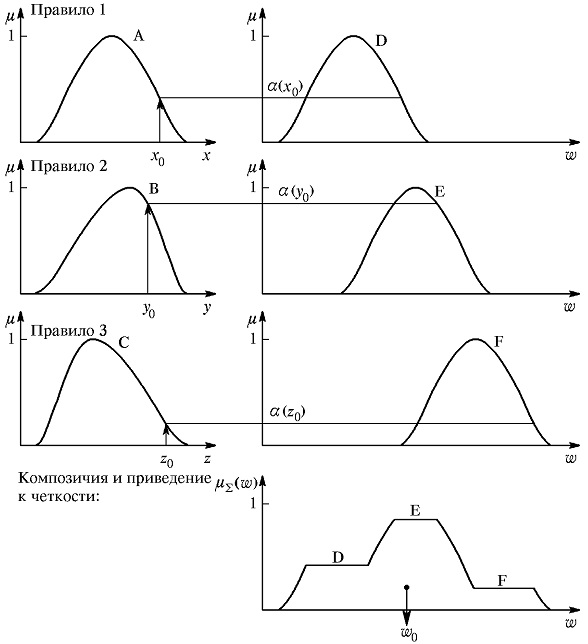
Мы помним, что каждое значение лингвистической переменной — это нечеткое множество, заданное функцией принадлежности. Обрабатывая каждое правило согласно текущим показателям ошибки:
Мы получаем в итоге композицию всех правил — некое нечеткое множество. Это и есть решение, которое принял наш нечеткие регулятор на основании введенных правил и текущих показателях. Это решение не подашь на вход контроллеров двигателей, поэтому нужна
Дефузификация — приведение к четкости
Опять же, существует несколько вариантов дефузифицировать нечеткое множество, но мы выберем самое простое для понимания и алгоритмизации.
Это дискретный вариант центроидного метода. Где n — количество всех правил, zi -выходной сигнал каждого правила.αi это вычисление условий каждого правила для данных входных параметров.
Опять сложно и заумно, не люблю так, давайте на примере четвертого правила вычислим альфа.
Мы берем меру вхождения ошибки e в нечеткое множество «Большое отрицательное», берем меру вхождения первой разницы ошибок в нечеткое множество «Малое отрицательное» и находим их минимум. Минимум, т.к. оператор у нас нечеткая логическая И, а мы ввели этот оператор как минимум.
Вроде все!))
Мы получили число Z — являющееся управляющим воздействием на объект управления. Давайте напишем чуть-чуть программного кода)
Программная реализация нечеткого регулятора
Начнем с определения значений нечетких лингвистических переменных.
#define fVLN -125 //Очень большое отрицательное#define fLN -90 //Большое отрицательное#define fMN -55 //Среднее отрицательное#define fSN -20 //Малое отрицательное#define fNO 0 //Нулевое#define fSP 20 //Малое положительное#define fMP 55 //Среднее положительное#define fLP 90 //Большое положительное#define fVLP 125 //Очень сильное положительное |
Далее мы определяем структуру, которая будет содержать каждое наше правило.
struct rule{ int8_t fe; op_type op; int8_t fde; int8_t z;}; |
Теперь нужно определить функцию меры принадлежности переменной к определенному нечеткому множеству. Как мы определились — это будет функция Гаусса.
/*Степень принадлежности µÃ(x)в какой степени (мере) элемент x принадлежит нечёткому множеству Ã.\param[out] Мера принадлежности\param[in] х Элемент из Х \param[in] A Нечеткое множество Ã*/double mu(int8_t x, int8_t A){ return exp(-(pow(x-A,2)/(2*pow(30,2))));} |
Ну и запишем еще вспомогательную функцию для добавления правил
/*Добавить правила к регулятору\param[out] \param[in] fe значение лингвистической переменной "отклонение" для ошибки\param[in] op оператор И / ИЛИ\param[in] fde значение лингвистической переменной "отклонение" первой разности ошибки\param[in] z значение лингвистической переменной "воздействие"*/void addrule(int8_t fe,op_type op, int8_t fde, int8_t z){ rules[numofrules].fe = fe; rules[numofrules].op = op; rules[numofrules].fde = fde; rules[numofrules].z = z; numofrules++;} |
Ну вроде все! Можно экспериментировать, добавим описанные выше правила
addrule(fNO,AND,fNO,fNO);addrule(fVLN,OR,fVLN,fVLP);addrule(fVLP,OR,fVLP,fVLN);addrule(fLN,AND,fSN,fVLP);addrule(fLP,AND,fSP,fVLN);addrule(fSN,AND,fSN,fSP);addrule(fSP,AND,fSP,fSN); |
И запустим цикл по правилам, чтоб вычислить нужное управляющее воздействие
/*Реализация нечеткого регулятора согласно правил\param[out] Управляющее воздействие\param[in] e текущая ошибка\param[in] de первая разница ошибок*/double processRules( int8_t e,int8_t de){ double summ_alpha_c = 0, summ_alpha = 0; // цикл по правилам for(int i =0; i<(int)(numofrules);i++){ double alpha = 0, mue = 0, mude = 0; // степень соответствия ошибки нечеткому множеству fe для i-го правила mue = mu(e,rules[i].fe); // степень соответствия первой разности ошибки нечеткому множеству fde для i-го правила mude = mu(de,rules[i].fde); // применяем логический оператор И/ИЛИ alpha = rules[i].op==0?MIN(mue,mude):MAX(mue,mude); // числитель и знаменатель для дискретного варианта // центроидного метода приведения к четкости summ_alpha_c += (alpha*rules[i].z); summ_alpha += alpha; } // вычисляем воздействие на объект управления return summ_alpha_c/summ_alpha;} |
Теперь точно все, тестируем)
// от оъекта управления int8_t e = 50; int8_t de = 0; printf("e=%i; deltae=%i Z=%f\n",e,de,processRules(e,de)); |
На выходе получаем
e=50; deltae=0 Z=-50.133715
Иными словами у нас несильный правый крен и регулятор предлагает компенсировать соразмерным левым креном.
Еще тест:
// от оъекта управления int8_t e = 50; int8_t de = 30; printf("e=%i; deltae=%i Z=%f\n",e,de,processRules(e,de)); |
На выходе получаем
e=50; deltae=30 Z=-62.406541
Регулятор понял, что ситуация ухудшается, предыдущая ошибка была 20, а текущая — 50. Поэтому он предлагает действовать более радикально и подать воздействие -62.
Ну и еще разок:
// от оъекта управления int8_t e = 50; int8_t de = -30; printf("e=%i; deltae=%i Z=%f\n",e,de,processRules(e,de)); |
На выходе получаем
e=50; deltae=30 Z=-34.527540
Тут регулятор понял, что есть результат регулирования, причем хороший — было 80, стало 50. Поэтому он предлагает понизить управляющее воздействие, дабы избежать перерегулирования.
Заключение
Коллеги, мы реализовали регулятор БПЛА на нечеткой логике, используя нечеткий вывод. Объем материала большой, но, как вы убедились, ничего сложного в самой математике нет.
Во всей реализации регулятора, главное определить набор правил, исходя из простой логики и/или из экспертного мнения.
На этом мы завершаем выпуск) В следующий раз уже будем прикручивать наш fuzzy controller к реализуемому автопилоту. Попробуем в автоматическом режиме поддерживать нужный крен!)
Всем удачи и до связи!