Коллеги, сегодня мы разберемся с таким инструментом, как Нечеткий регулятор.
Но, для начала, немного математики, совсем чуть-чуть)
Нечеткая логика
Итак, что же из себя представляет нечеткая логика / fuzzy logic — это раздел математики, являющийся расширением классической логики. Она основывается на понятии нечёткого множества. В свою очередь нечеткое множество — это, по-сути, функция принадлежности элемента к отрезку [0, 1], а не только 0 или 1, как в классической логике.
Звучит очень сложно, но сейчас разберем все на примере.
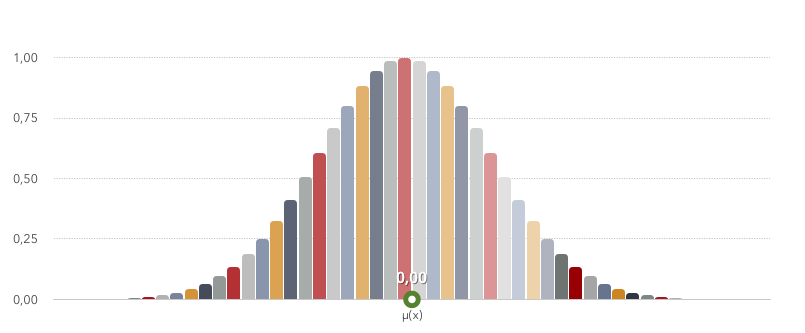
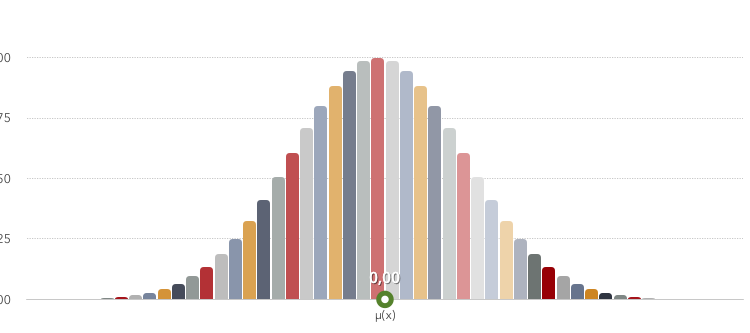
Вот перед вами нечеткое множество «Ноль» и мера принадлежности элементов отрезка[-1,1] к данному нечеткому множеству . Как вы видим само число 0 принадлежит построенному множеству с мерой 1(истина), а -1 и 1 принадлежат с мерой 0(ложь) — то-есть не принадлежат))) А вот элементы -0.1 и 0.1 принадлежат этому множеству с мерой 0.9 и т.д.
Функция принадлежности / membership function
Функция, образовавшая данное множество, называется функцией принадлежности и, вообще, может быть другой, но в данном примере:
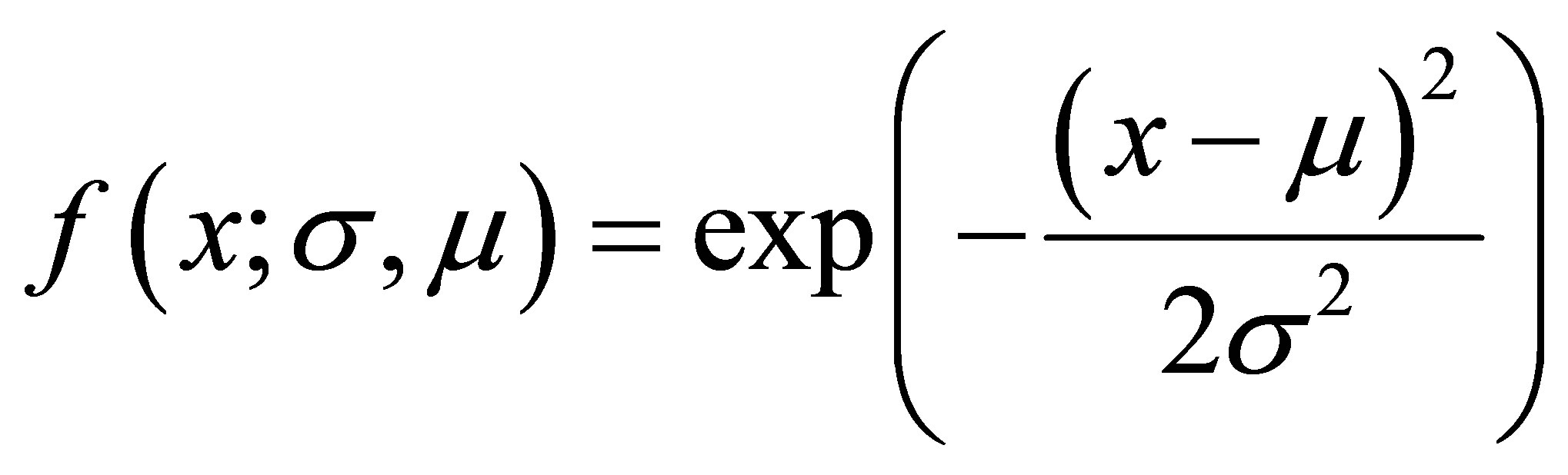
Это Функция Гаусса (Gaussian membership function), ее мы и будем использовать в нашем нечетком регуляторе. Тут нужно пояснить, что «мю» — это центр распределения(в нашем примере — 0). А «сигма» — это ширина, базис, функции(тут 0.3). Чем больше базис, тем больше элементов базового множества X включается в наше нечеткое подмножество.
Нечеткая логическая переменная
Итак, мы практически рассмотрели еще одно понятие Нечеткая логическая переменная — это переменная которая имеет имя(в нашем примере «Ноль»), имеет область определения(у нас отрезок [-1,1]), и имеет нечеткое подмножество этой области, определенное функцией меры вхождения(соответствия) элементов из области определения в нечеткое подмножество.
Если отбросить все лишнее, то Нечеткая логическая переменная задается функцией принадлежности.
Итак, хватит разминаться, далее пора заняться математикой)
Логические операции над нечеткими множествами
Возьмем два нечетких множества A и B, и введем операции над ними :
Нечеткое логическое И: A & B = MIN(A,B);
ИЛИ: A | B = MAX(A,B);
Отрицание: ¬ A = 1 — A;
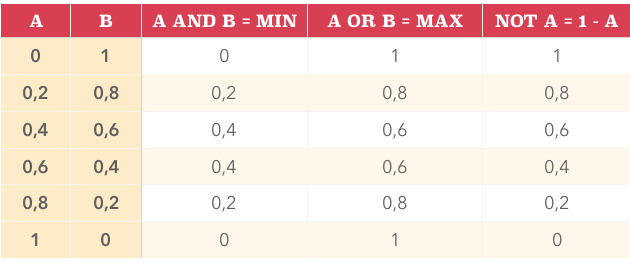
Построим, для наглядности, таблицу истинности:
Как мы видим, таблица полностью совпадает со знакомой нам в своей классической части.
Далее, давайте введем еще одно очень важное для нашей задачи понятие:
Лингвистические переменные и их значения
Нечеткая лингвистическая переменная — переменная, которая может принимать значения фраз из естественного языка, которые, в свою очередь, являются нечеткими множествами.
Опять что-то непонятное)
Давайте на примере: лингвистическая переменная «Крен«.(О! уже ближе к реалиям задачи))
Определим ее значения: «Левый«, «Нулевой«, «Правый«.
Из определения, значения должны быть нечеткими множествами, исходя из этого, рассмотренное выше нечеткое множество «Ноль» можно рассматривать, как значение «Нулевой» Лингвистической переменной «Крен».
Если крен у нас 0.1 или -0.1 (они входят в наше нечеткое множество со значениями 0.9), то откровенно говоря, крен все еще нулевой, нет смысла его исправлять, как и значения ± 0.2. А вот значение крена 0.7 будет входить в наше множество «Нулевой» крен, со значением 0.3, иными словами — это совсем не нулевой крен, а скорее правый.
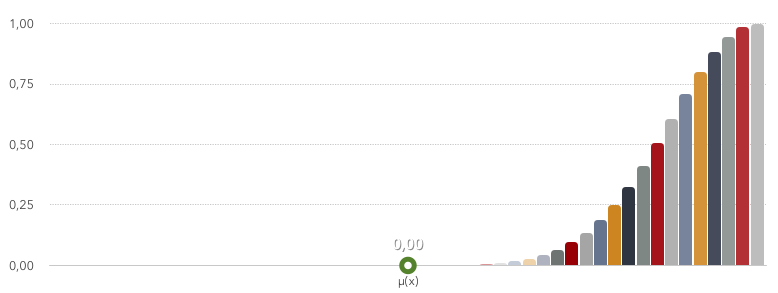
Давайте составим нечеткое множество «Правый», для этого в функции принадлежности Гаусса возьмем «мю» равное 1 — хороший правый крен. Вот какой график распределения у нас теперь получится:
Теперь крен со значением 0 вообще не входит в данное множество, зато крен со значением 1 входит в позиции Истина, со степенью вхождения 1.
Так же строятся остальные нечеткие лингвистические переменные, нужные в данной конкретной задаче.
На этом теория заканчивается, в следующей части мы займемся решением задачи построения нечеткого регулятора. Также запрограммируем готовое решение на языке C.
Оставайтесь на связи)